洛必达法则简单讲解（高等数学——详解洛必达法则）

用处

我们学习的目的往往很朴素，就是学以致用，之前的时候我总觉得这种想法有些现实，后来我发现很多学了不能致用的知识都忘得差不多了。所以尽管我们的心态要放好，但是操作的时候可以实际一些，先从用处入手，也许能更好地理解也说不定。

洛必达法则的应用场景非常简单，就是能解决一些一下子无法求解的极限问题。不知道大家有没有发现，不管在什么领域，总有一些一下子无法解决的问题。伴随着对这些问题的研究，我们的技术和理论在不断的进步，工作在不断地简化，效率越来越高。无论是数学上某个领域的突破还是计算机当中某些工具的迭代和演进，莫不如此。

我们之前介绍极限的文章当中讲过一道例题：

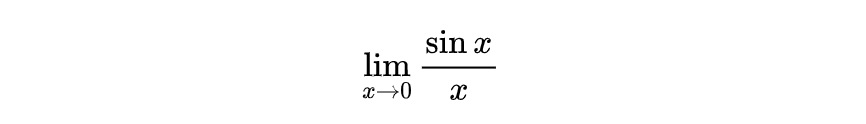
在这题当中，由于x趋向于0的时候， sinx 和x都趋向于0，我们要计算0除以0的结果，当时为了解决这个问题，我们用上了夹逼法，对它进行了缩放之后才得到了极限。类似的极限还有很多，本质上来说问题在于当分子和分母都趋向于0时，我们很难计算得到结果。

再比如x/x^2，这个问题很简单，只要进行约分，那么就是 1/x 的极限，x趋向于0时，显然 1/x 趋向于无穷大。但如果不约分呢？它就是一个极限0除以极限0的问题，和上面的结果不同，它的比值结果是无穷大。

洛必达法则就是为了解决上述这些极限问题而出现的。

定义

洛必达法则的本质是一个定理，它规定，如果一个形如

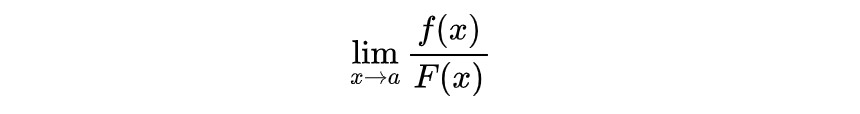
的极限，如果它满足：

1. x趋向于常数a时，函数f(x)和F(x)都趋向于0
2. 在点a的去心邻域内，f(x)和F(x)的导数都存在，并且F'(x) 不等于 0
3. 存在 lim f'(x)/F'(x)

那么：

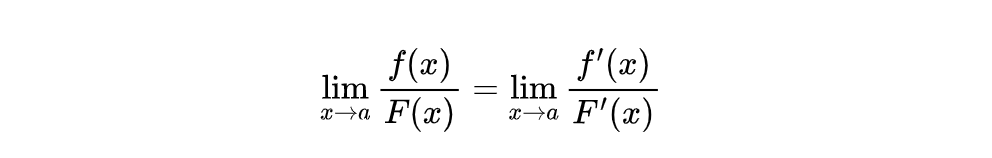
也就是当变量趋向于一个常数时，如果分子分母函数的导数存在，那么我们可以用导数的极限比值来代替原函数的比值。

我们来试着证明这个定理，如果你回顾了微分中值定理的话，这个定理的证明非常简单。我们来试一下证明。

证明

由于函数在a点的去心邻域可导，也就是说函数在这个a的去心邻域内连续。那么我们套用柯西中值定理，在x趋向于a时，可以得到在区间(a, x)内找到一个点ξ，使得：

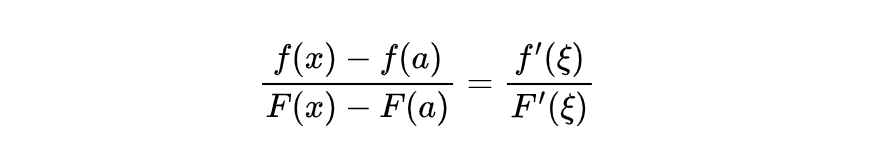
到这里还差一点，因为还少了一个条件，书上的解释是由于函数比值的极限与函数值无关，所以可以假设f(a)和F(a)等于0。我个人觉得这样有些不厚道，就和证明过程里写易证、易得是一样的。其实我们只要将这两做差，证明一下差值等于0即可。

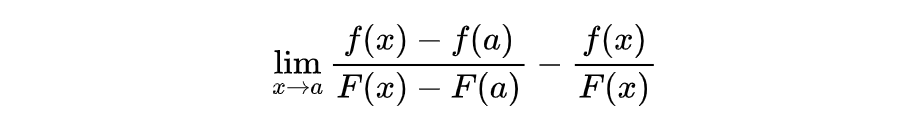
通分之后，可以得到：

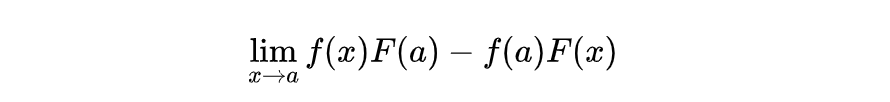
到这里，不难看出来，当x趋向于a的时候，上面的差值趋向于0，所以：

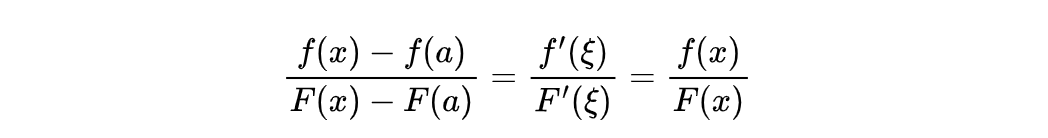
由于x趋向于a的时候，ξ也趋向于a，那么我们就得到了：

尝试

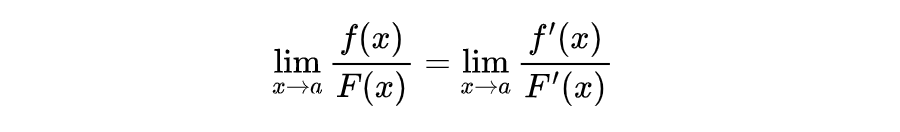
我们学会了洛必达法则之后就可以活学活用来解决一些比较棘手的极限问题了。比如刚才我们举的例子就再也不是问题了。

再来看一个：

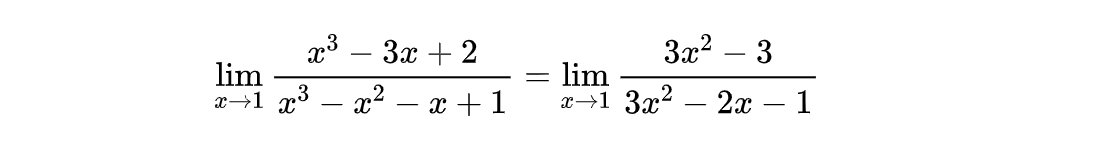
到这里我们还是无法得到结果，看样子是卡壳了。但是别着急，洛必达法则是可以嵌套使用的。原因很简单，只要我们把 f'(x) 看成是新的 f(x)，F'(x) 看成是新的 F(x)，只要新的函数还满足洛必达法则的使用条件，那么我们可以继续使用洛必达法则。也就是说，我们可以得到：

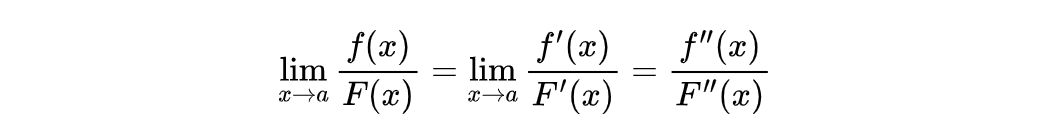
当然使用嵌套也存在前提，前提就是二阶导数存在，并且 F''(x) 不等于0。同样的道理，只要高阶导数存在，并且分母不为0，我们可以一直嵌套下去。所以洛必达法则也可以称为套娃法则。有了套娃之后，问题就简单了，上面的问题我们只要往下套就行了：

变形

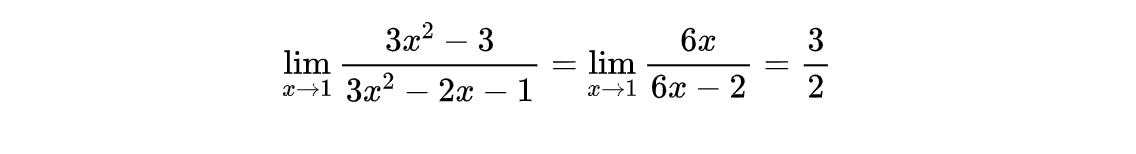
除了套娃之外，洛必达法则还存在一个著名的变形。前面讨论的使用范畴都是在x趋向于一个常数的情况下的，其实在一些特殊的情况下，当x趋向于正无穷时，我们一样可以套用洛必达法则。和基础版本一样，同样需要函数f(x)和F(x)满足一些条件：

1. x趋向于正无穷时，f(x)和F(x)同时趋向于0或者无穷
2. 存在N使得当|x| > N时，f'(x)和F'(x)都存在，并且F'(x)不等于0
3. 存在lim f'(x)/F'(x)

我们来看个例子：

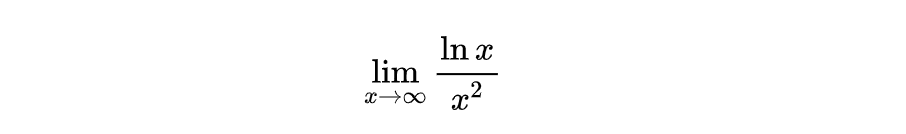
我们可以看出来，当x趋向于无穷的时候，分子分母都趋向于无穷。所以我们可以使用洛必达法则：

总结

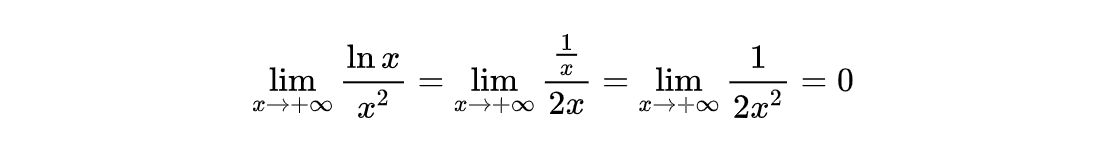
洛必达法则在高数当中非常重要，尤其是在计算极限的时候，很多看起来很麻烦的极限在经过洛必达法则的转换之后说不定就简单得多。

但是关于洛必达法则使用的限制看起来有些麻烦，其实我们只需要牢记两点即可。第一点是不管x趋向于什么值，只要保证分子分母同时趋向于0或者是无穷，并且导数存在，且分母的导数不为0即可。也就是说如果分子分母的极限不同时为0或者无穷大，则不能使用洛必达法则。这一点一定要牢记，因为在我们多次使用洛必达法则的过程当中，很有可能出现分子分母不在满足这个条件的情况，我们在使用的时候一定要铭记。